Prototype translater from a μ-calculus over finite trees to tree automata
Short Version
If you have ocaml, menhir, bash and g++ just download automata.tar untar it, look at the source code of our prototype in gen/ or just run the benchmark with bash do_everything.sh.Long Version
This page is still under construction but you can find the source of our mu-calculs to automata here. You can also download the whole folder at the address automata.tar. In this folder, you will find:- gen contains the source code of the actual translation. You'll need OCaml and menhir to compile it! Compile it with make and then run it with ./solver FORMULA_FILE compress stats !
- A bash script do_everyting.sh will compile our prototype and a program for intersecting two automata then it will run the benchmarks presented in the paper; forms contains some example formulae;
- intersect contains the source code to intersect to automata in the /trad/ format, you will need g++ to compile it;
- translateXPath contains the XPathMark benchmark and some shell scripts to run them;
- gen_form contains the formulas of the 2nd benchmark.
a4μ source code
The source is stored on inria gitlab page : https://gitlab.inria.fr/jachiet/a4mu
The source code of the translation to automata is available as a tar file source_solver.tar or you can browse directly the directory source_solver
Organization
The prototype translator
The sources of the prototype can be found in the folder gen. The interesting files of this folder are:
- Auto.ml contains everything related to automata.
- Bf.ml is used to represent formulae once the formula has been normalized (only P_j or <a>f(V1,…,Vn).
- Mu.ml is a module for representing general formulae.
- Sol.ml is our symbolic representation of types.
- lexer.mll and parser.mly are used to parser the input formula.
Intersecting
The directory intersect contains an algorithm that takes two automata in the standard input and prints out "EMPTY" when the two automata contain no common tree and it prints out "NON EMPTY" followed by an example tree otherwise.
Forms
The directory forms contains some examples formulae.
Example
The directory example contains an automaton example.auto that accepts any tree. This automaton is used by the script get_example.sh to print an example solution for a formula (see manual).
translateXPath
The directory translateXPath contains the benchmark that tests the lineage of n 'tr' elements against the xhtml dtd.
a4μ manuel
Compiling
The solver requires the ocaml compiler, menhir and make to compile. The command make in the source folder trad should produce an executable solver binary. To use the intersection, you will also need to run make in the folder intersect folder.Formulae
The language of input formulae is:φ = φ & φ̩ | φ | φ̩ | let $var = φ, …, $var = φ in $var | mu $var . φ | mu var . φ | <1> φ | <2> φ | <-1> φ | <-2> φ | $var | atom | (φ) | T | ~φWarning: the let with more than one variable is still beta.
Solving a formula
Provided FILE is file containing a valid formulasolver FILEwill output the automaton for the formula in FILE. The solver commands accepts several arguments:
- compress makes the compiler suppose that atomic propositions are mutually exclusive and internally use a binary encoding of atomics;
- lean print the lean before solving the formula;
-
plunge indicates to the solver to solve
let $x = <1> $x | <2> $x | φ in $x
- determinize determinze the automaton before printing it;
- debug is a verbose option to print information about the solving process;
- stats print general information about the solving process.
Output format (for non deterministic tree automaton)
The solver output starts by a line containing an integer n followed by n strings corresponding of the n labels used by the automaton. _other is a special label. When compression is used, it indicates any other label than those appearing in the formula. When the compression is not used it indicates that a transition where no atomics are true. The second line contains 5 integers T s1 s2 f R. States of the automaton are integers between 0 and T. si is the state representing a i-leaf. f is the unique final state. Finally, R is the number of transitions. In the current version we have si=i-1. Each of the R following lines contains a string l (the label) and tree integers e1 e2 r. This represents a transition where ei is the i-child, r is the parent state and l is the label of the transition.
Intersection and example solutions
You can intersect two automata using the inter binary in the folder intersect. The inter binary waits for automata on its standard. Example (ran in /trad/):./solver ../forms/multi compress | cat ../example/example.auto - | ./intersect/interIntersecting with the automaton that accepts anything is a fast way to get example solutions for a formula so we have bundled it into the script example/get_example.sh. Our previous example become:
./solver ../forms/multi compress | ../example/get_example.sh
a4μ benchmark
We experimented our prototype in different configurations. Here are the results.
Un = (//tr/*)^n
We tested our solver in presence of two DTD (XHTML strict and XHTML basic) in presence of the formula that tests if there is a lineage of n nodes tr.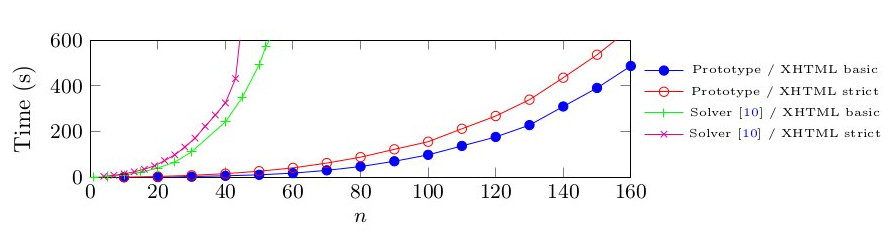
Vn= (/tr/[^tr]*)^n
As a comparison here is the time spent to compute the automaton for the XPath Vn which corresponds to check if there is a lineage of exactly n tr (and for which a DTA has necessarily at least 2^n states) against the DTD xhtml strict (thus the non-exponential time for small value of n).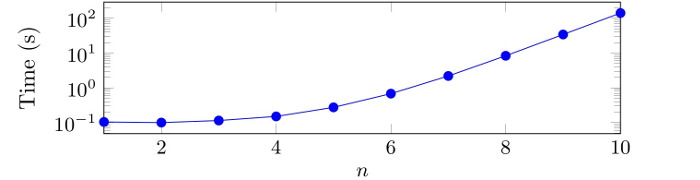
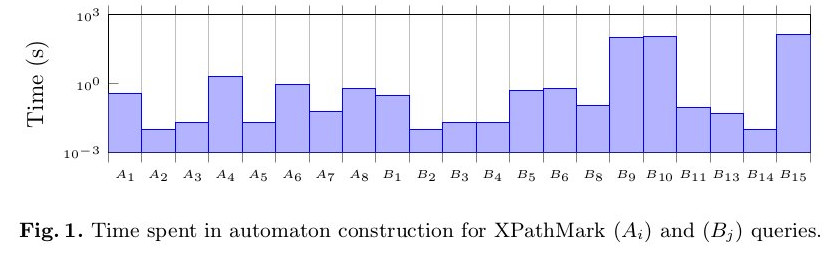
XPathMark benchmark
We tested our translation against the XPathMark benchmark. We limited ourselves to queries translatable in our μ-calculus.